Цели и задачи регрессионного тестирования

При корректировках программы необходимо гарантировать сохранение качества. Для этого используется регрессионное тестирование - дорогостоящая, но необходимая деятельность в рамках этапа сопровождения, направленная на перепроверку корректности измененной программы. В соответствии со стандартным определением, регрессионное тестирование - это выборочное тестирование, позволяющее убедиться, что изменения не вызвали нежелательных побочных эффектов, или что измененная система по-прежнему соответствует требованиям.

Главной задачей этапа сопровождения является реализация систематического процесса обработки изменений в коде. После каждой модификации программы необходимо удостовериться, что на функциональность программы не оказал влияния модифицированный код. Если такое влияние обнаружено, говорят о регрессионном дефекте. Для регрессионного тестирования функциональных возможностей, изменение которых не планировалось, используются ранее разработанные тесты. Одна из целей регрессионного тестирования состоит в том, чтобы, в соответствии с используемым критерием покрытия кода (например, критерием покрытия потока операторов или потока данных), гарантировать тот же уровень покрытия, что и при полном повторном тестировании программы. Для этого необходимо запускать тесты, относящиеся к измененным областям кода или функциональным возможностям.

Пусть T = {t1, t2, ..., tN} - множество из N тестов, используемое при первичной разработке программы P, а T'

T - подмножество регрессионных тестов для тестирования новой версии программы P'. Информация о покрытии кода, обеспечиваемом T', позволяет указать блоки P', требующие дополнительного тестирования, для чего может потребоваться повторный запуск некоторых тестов из множества T

T', или даже создание T'' - набора новых тестов для P' - и обновление T.

Другая цель регрессионного тестирования состоит в том, чтобы удостовериться, что программа функционирует в соответствии со своей спецификацией, и что изменения не привели к внесению новых ошибок в ранее протестированный код.

Эта цель всегда может быть достигнута повторным выполнением всех тестов регрессионного набора, но более перспективно отсеивать тесты, на которых выходные данные модифицированной и старой программы не могут различаться. Результаты сравнения выборочных методов и метода повторного прогона всех тестов приведены в таблица 11.1.

Таблица 11.1. Выборочное регрессионное тестирование и повторный прогон всех тестов.Повторный прогон всех тестовВыборочное регрессионное тестирование

Прост в реализации	Требует дополнительных расходов при внедрении
Дорогостоящий и неэффективный	Способно уменьшать расходы за счет исключения лишних тестов
Обнаруживает все ошибки, которые были бы найдены при исходном тестировании	Может приводить к пропуску ошибок

Задача отбора тестов из набора T для заданной программы P и измененной версии этой программы P' состоит в выборе подмножества T'идеальное

T для повторного запуска на измененной программе P', где T'идеальное = {t

T | P'(t)

P(t)}. Так как выходные данные P и P' для тестов из множества T

T'идеальное заведомо одинаковы, нет необходимости выполнять ни один из этих тестов на P'. В общем случае, в отсутствие динамической информации о выполнении P и P' не существует методики вычисления множества T'идеальное для произвольных множеств P, P' и T. Это следует из отсутствия общего решения проблемы останова, состоящей в невозможности создания в общем случае алгоритма, дающего ответ на вопрос, завершается ли когда-либо произвольная программа P для заданных значений входных данных. На практике создание T'идеальное возможно только путем выполнения на инструментированной версии P' каждого регрессионного теста, чего и хочется избежать.

Реалистичный вариант решения задачи выборочного регрессионного тестирования состоит в получении полезной информации по результатам выполнения P и объединения этой информации с данными статического анализа для получения множества T'реальное в виде аппроксимации T'идеальное. Этот подход применяется во всех известных выборочных методах регрессионного тестирования, основанных на анализе кода.

Множество T' реальное должно включать все тесты из T, активирующие измененный код, и не включать никаких других тестов, то есть тест t

T входит в T'реальное тогда и только тогда, когда t задействует код P в точке, где в P' код был удален или изменен, или где был добавлен новый код.

Если некоторый тест t задействует в P тот же код, что и в P', выходные данные P и P' для t различаться не будут. Из этого следует, что если P(t)

P'(t), t должен задействовать некоторый код, измененный в P' по отношению к P, то есть должно выполняться отношение t

T'реальное. С другой стороны, поскольку не каждое выполнение измененного кода отражается на выходных значениях теста, могут существовать некоторые такие t

T'реальное, что P(t) = P'(t). Таким образом, T'реальное содержит T'идеальное целиком и может использоваться в качестве его альтернативы без ущерба для качества тестируемого программного продукта.

Важной задачей регрессионного тестирования является также уменьшение стоимости и сокращение времени выполнения тестов.

Рассмотрим отбор тестов на примере рис. 11.1. Код, покрываемый тестами, выделен цветом и штриховкой. Легко заметить, что код, покрываемый тестом 1, не изменился с предыдущей версии, следовательно, повторное выполнение теста 1 не требуется. Напротив, код, покрываемый тестами 2, 3 и 4, изменился; следовательно, требуется их повторный запуск.

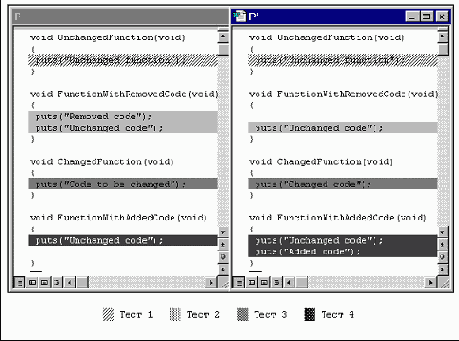
Рис. 11.1. Отбор тестов для множества T'.

Содержание раздела